When I listen to the callers and the questions they pose to Tom and Ray, I am frequently astounded by how little some people understand about the inner workings of their cars and trucks. Even though they can operate their vehicles, many of them haven't the foggiest idea what makes it work or why sometimes it doesn't work as expected.
But, then, this isn't really much different from how many people function mathematically. In many cases, they may know a rule that gets them a "right answer," But they have no idea why it works. Further, if the conditions vary from the expected and the "recipe" fails, they are totally unable to reason a resolution to their problem on their own.
I used to do an activity with middle-schoolers in which I placed 24 markers of some sort on the overhead projector and asked someone to illustrate 24 divided by 3. Invariably, the first volunteer would remove all but 8 of the markers, because 24 divided by 3 equals 8.
After some coaxing and cajoling, someone would eventually realize that dividing 24 by 3 means that 24 is split into 3 equal groups of 8 (or 8 groups of 3).
Now, there is some understanding of what division means. Not just that there is a memorizable fact, 6/3=2, but WHY you get 2 when you divide 6 by 3.
Eight divided by 3 means to split 8 into 3 equal groups. Of course, this isn't possible without either allowing leftovers (a remainder) or using fractional pieces. Kids can see division as a physical process and what the logical consequences of that process might be. What would happened if you divided 5 into 2 equal groups?
Using this concept it is much easier to explain why division by zero is not valid. How do you group several things into 0 groups, or into groups of 0? It's nonsensical to try to do so!
I very strongly believe that kids need to see and represent mathematical concepts visually with drawings and diagrams and physically using objects and models. They need to ”dirty their hands” with math if they are to get a feel for the way it works.
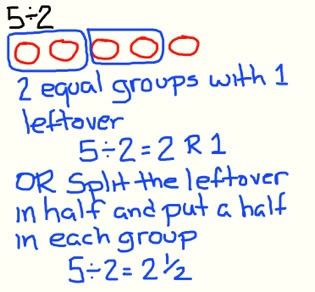
No comments:
Post a Comment